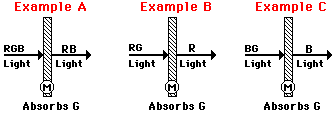Distance and displacement are two quantities that may seem to mean the
same thing yet have distinctly different definitions and meanings.
-
Distance is a scalar quantity that refers to "how much ground an object has covered" during its motion.
-
Displacement is a vector quantity that refers to "how far out of place an object is"; it is the object's overall change in position.
To test your understanding of this distinction, consider the motion
depicted in the diagram below. A physics teacher walks 4 meters East, 2
meters South, 4 meters West, and finally 2 meters North.
Even though the physics teacher has walked a total distance of 12
meters, her displacement is 0 meters. During the course of her motion,
she has "covered 12 meters of ground" (distance = 12 m). Yet when she is
finished walking, she is not "out of place" - i.e., there is no
displacement for her motion (displacement = 0 m). Displacement, being a
vector quantity, must give attention to direction. The 4 meters east cancels the 4 meters west; and the 2 meters south cancels the 2 meters north. Vector quantities such as displacement are direction aware.
Scalar quantities such as distance are ignorant of direction. In
determining the overall distance traveled by the physics teachers, the
various directions of motion can be ignored.
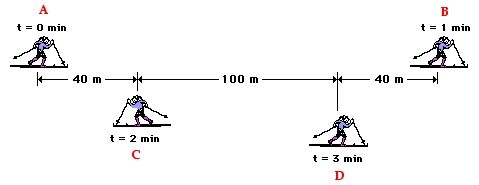
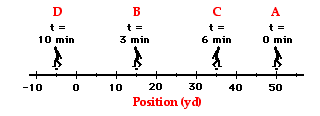
Now consider another example. The diagram below shows the position of a
cross-country skier at various times. At each of the indicated times,
the skier turns around and reverses the direction of travel. In other
words, the skier moves from A to B to C to D.
 Use
the diagram to determine the resulting displacement and the distance
traveled by the skier during these three minutes. Then click the button
to see the answer.
Use
the diagram to determine the resulting displacement and the distance
traveled by the skier during these three minutes. Then click the button
to see the answer.
As a final example, consider a football coach pacing back and forth
along the sidelines. The diagram below shows several of coach's
positions at various times. At each marked position, the coach makes a
"U-turn" and moves in the opposite direction. In other words, the coach
moves from position A to B to C to D.
 What is the coach's resulting displacement and distance of travel? Click the button to see the answer.
What is the coach's resulting displacement and distance of travel? Click the button to see the answer.
To understand the distinction between distance and displacement, you must know the definitions. You must also know that a vector quantity such as displacement is direction-aware and a scalar quantity such as distance is ignorant of direction.
When an object changes its direction of motion, displacement takes this
direction change into account; heading the opposite direction
effectively begins to cancel whatever displacement there once was.
Check Your Understanding
1. What is the displacement of the cross-country team if they begin at the school, run 10 miles and finish back at the school?
2. What is the distance and the displacement of the race car drivers in the Indy 500?
Just as distance and displacement have distinctly different meanings (despite their similarities), so do speed and velocity. Speed is a scalar quantity
that refers to "how fast an object is moving." Speed can be thought of
as the rate at which an object covers distance. A fast-moving object has
a high speed and covers a relatively large distance in a short amount
of time. Contrast this to a slow-moving object that has a low speed; it
covers a relatively small amount of distance in the same amount of time.
An object with no movement at all has a zero speed.
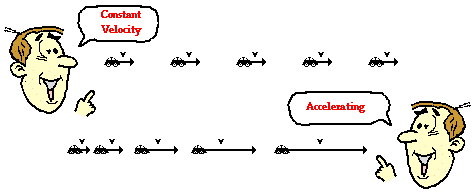
Velocity as a Vector Quantity
Velocity is a vector quantity
that refers to "the rate at which an object changes its position."
Imagine a person moving rapidly - one step forward and one step back -
always returning to the original starting position. While this might
result in a frenzy of activity, it would result in a zero velocity.
Because the person always returns to the original position, the motion
would never result in a change in position. Since velocity is defined as
the rate at which the position changes, this motion results in zero
velocity. If a person in motion wishes to maximize their velocity, then
that person must make every effort to maximize the amount that they are
displaced from their original position. Every step must go into moving
that person further from where he or she started. For certain, the
person should never change directions and begin to return to the
starting position.
Velocity is a vector quantity. As such, velocity is direction aware.
When evaluating the velocity of an object, one must keep track of
direction. It would not be enough to say that an object has a velocity
of 55 mi/hr. One must include direction information in order to fully
describe the velocity of the object. For instance, you must describe an
object's velocity as being 55 mi/hr, east. This is one of the essential differences between speed and velocity. Speed is a scalar quantity and does not keep track of direction; velocity is a vector quantity and is direction aware.
 Determining the Direction of the Velocity Vector
Determining the Direction of the Velocity Vector
The task of describing the direction of the velocity vector is easy. The
direction of the velocity vector is simply the same as the direction
that an object is moving. It would not matter whether the object is
speeding up or slowing down. If an object is moving rightwards, then its
velocity is described as being rightwards. If an object is moving
downwards, then its velocity is described as being downwards. So an
airplane moving towards the west with a speed of 300 mi/hr has a
velocity of 300 mi/hr, west. Note that speed has no direction (it is a
scalar) and the velocity at any instant is simply the speed value with a
direction.
Calculating Average Speed and Average Velocity
As an object moves, it often undergoes changes in speed. For example,
during an average trip to school, there are many changes in speed.
Rather than the speed-o-meter maintaining a steady reading, the needle
constantly moves up and down to reflect the stopping and starting and
the accelerating and decelerating. One instant, the car may be moving at
50 mi/hr and another instant, it might be stopped (i.e., 0 mi/hr). Yet
during the trip to school the person might average 32 mi/hr. The average
speed during an entire motion can be thought of as the average of all
speedometer readings. If the speedometer readings could be collected at
1-second intervals (or 0.1-second intervals or ... ) and then averaged
together, the average speed could be determined. Now that would be a lot
of work. And fortunately, there is a shortcut. Read on.
The average speed during the course of a motion is often computed using the following formula:
In contrast, the average velocity is often computed using this formula
Let's begin implementing our understanding of these formulas with the following problem:
Q: While on vacation, Lisa Carr traveled a total distance of 440 miles. Her trip took 8 hours. What was her average speed?
To compute her average speed, we simply divide the distance of travel by the time of travel.
That was easy! Lisa Carr averaged a speed of 55 miles per hour. She may
not have been traveling at a constant speed of 55 mi/hr. She
undoubtedly, was stopped at some instant in time (perhaps for a bathroom
break or for lunch) and she probably was going 65 mi/hr at other
instants in time. Yet, she averaged a speed of 55 miles per hour. The
above formula represents a shortcut method of determining the average
speed of an object.
Average Speed versus Instantaneous Speed
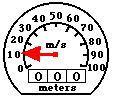 Since
a moving object often changes its speed during its motion, it is common
to distinguish between the average speed and the instantaneous speed.
The distinction is as follows.
Since
a moving object often changes its speed during its motion, it is common
to distinguish between the average speed and the instantaneous speed.
The distinction is as follows.
-
Instantaneous Speed - the speed at any given instant in time.
-
Average Speed - the average of all instantaneous speeds; found simply by a distance/time ratio.
You might think of the instantaneous speed as the speed that the
speedometer reads at any given instant in time and the average speed as
the average of all the speedometer readings during the course of the
trip. Since the task of averaging speedometer readings would be quite
complicated (and maybe even dangerous), the average speed is more
commonly calculated as the distance/time ratio.
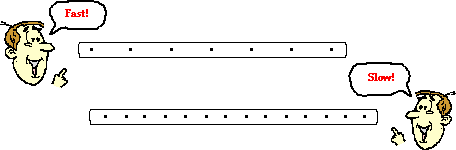
Moving objects don't always travel with erratic and changing speeds.
Occasionally, an object will move at a steady rate with a constant
speed. That is, the object will cover the same distance every regular
interval of time. For instance, a cross-country runner might be running
with a constant speed of 6 m/s in a straight line for several minutes.
If her speed is constant, then the distance traveled every second is the
same. The runner would cover a distance of 6 meters every second. If we
could measure her position (distance from an arbitrary starting point)
each second, then we would note that the position would be changing by 6
meters each second. This would be in stark contrast to an object that
is changing its speed. An object with a changing speed would be moving a
different distance each second. The data tables below depict objects
with constant and changing speed.

Now let's consider the motion of that physics teacher
again. The physics teacher walks 4 meters East, 2 meters South, 4
meters West, and finally 2 meters North. The entire motion lasted for 24
seconds. Determine the average speed and the average velocity.
The physics teacher walked a distance
of 12 meters in 24 seconds; thus, her average speed was 0.50 m/s.
However, since her displacement is 0 meters, her average velocity is 0
m/s. Remember that the displacement
refers to the change in position and the velocity is based upon this
position change. In this case of the teacher's motion, there is a
position change of 0 meters and thus an average velocity of 0 m/s.
Here is another example similar to what was seen before in the discussion of distance and displacement.
The diagram below shows the position of a cross-country skier at
various times. At each of the indicated times, the skier turns around
and reverses the direction of travel. In other words, the skier moves
from A to B to C to D.
 1.Use
the diagram to determine the average speed and the average velocity of
the skier during these three minutes. When finished, click the button to
view the answer.
1.Use
the diagram to determine the average speed and the average velocity of
the skier during these three minutes. When finished, click the button to
view the answer.
As a last example, consider a football coach pacing back and forth along
the sidelines. The diagram below shows several of coach's positions at
various times. At each marked position, the coach makes a "U-turn" and
moves in the opposite direction. In other words, the coach moves from
position A to B to C to D.
 2.What is the coach's average speed and average velocity? When finished, click the button to view the answer.
2.What is the coach's average speed and average velocity? When finished, click the button to view the answer.
In conclusion, speed and velocity are kinematic quantities that have distinctly different definitions. Speed, being a scalar quantity, is the rate at which an object covers distance. The average speed is the distance (a scalar quantity) per time ratio. Speed is ignorant of direction. On the other hand, velocity is a vector quantity; it is direction-aware. Velocity is the rate at which the position changes. The average velocity is the displacement or position change (a vector quantity) per time ratio.
The final mathematical quantity discussed in Lesson 1 is acceleration.
An often confused quantity, acceleration has a meaning much different
than the meaning associated with it by sports announcers and other
individuals. The definition of acceleration is:
-
Acceleration is a vector quantity that is defined as the rate at which an object changes its velocity. An object is accelerating if it is changing its velocity.
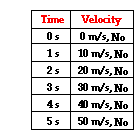 Sports
announcers will occasionally say that a person is accelerating if
he/she is moving fast. Yet acceleration has nothing to do with going
fast. A person can be moving very fast and still not be accelerating.
Acceleration has to do with changing how fast an object is moving. If an
object is not changing its velocity, then the object is not
accelerating. The data at the right are representative of a
northward-moving accelerating object. The velocity is changing over the
course of time. In fact, the velocity is changing by a constant amount -
10 m/s - in each second of time. Anytime an object's velocity is
changing, the object is said to be accelerating; it has an acceleration.
Sports
announcers will occasionally say that a person is accelerating if
he/she is moving fast. Yet acceleration has nothing to do with going
fast. A person can be moving very fast and still not be accelerating.
Acceleration has to do with changing how fast an object is moving. If an
object is not changing its velocity, then the object is not
accelerating. The data at the right are representative of a
northward-moving accelerating object. The velocity is changing over the
course of time. In fact, the velocity is changing by a constant amount -
10 m/s - in each second of time. Anytime an object's velocity is
changing, the object is said to be accelerating; it has an acceleration.
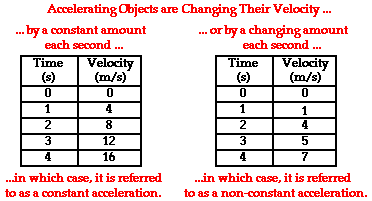
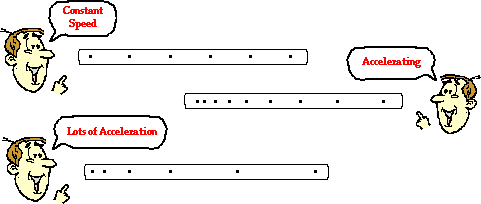
The Meaning of Constant Acceleration
Sometimes an accelerating object will change its velocity by the same
amount each second. As mentioned in the previous paragraph, the data
table above show an object changing its velocity by 10 m/s in each
consecutive second. This is referred to as a constant acceleration
since the velocity is changing by a constant amount each second. An
object with a constant acceleration should not be confused with an
object with a constant velocity. Don't be fooled! If an object is
changing its velocity -whether by a constant amount or a varying amount -
then it is an accelerating object. And an object with a constant
velocity is not accelerating. The data tables below depict motions of
objects with a constant acceleration and a changing acceleration. Note
that each object has a changing velocity.
Since accelerating objects are constantly changing their velocity, one
can say that the distance traveled/time is not a constant value. A
falling object for instance usually accelerates as it falls. If we were
to observe the motion of a free-falling object (free fall motion
will be discussed in detail later), we would observe that the object
averages a velocity of approximately 5 m/s in the first second,
approximately 15 m/s in the second second, approximately 25 m/s in the
third second, approximately 35 m/s in the fourth second, etc. Our
free-falling object would be constantly accelerating. Given these
average velocity values during each consecutive 1-second time interval,
we could say that the object would fall 5 meters in the first second, 15
meters in the second second (for a total distance of 20 meters), 25
meters in the third second (for a total distance of 45 meters), 35
meters in the fourth second (for a total distance of 80 meters after
four seconds). These numbers are summarized in the table below.
Time
Interval |
Velocity Change
During Interval |
Ave. Velocity
During Interval |
Distance Traveled
During Interval |
Total Distance Traveled from
0 s to End of Interval |
|
0 – 1.0 s |
0 to ~10 m/s |
~5 m/s |
~5 m |
~5 m |
|
1.0 – 2.0 s |
~10 to 20 m/s |
~15 m/s |
~15 m |
~20 m |
|
2.0 – 3.0 s |
~20 to 30 m/s |
~25 m/s |
~25 m |
~45 m |
|
3.0 – 4.0 s |
~30 to 40 m/s |
~35 m/s |
~35 m |
~80 m |
Note: The ~ symbol as used here means approximately.
This discussion illustrates that a free-falling object
that is accelerating at a constant rate will cover different distances
in each consecutive second. Further analysis of the first and last
columns of the data above reveal that there is a square relationship
between the total distance traveled and the time of travel for an object
starting from rest and moving with a constant acceleration. The total
distance traveled is directly proportional to the square of the time. As
such, if an object travels for twice the time, it will cover four times
(2^2) the distance; the total distance traveled after two seconds is
four times the total distance traveled after one second. If an object
travels for three times the time, then it will cover nine times (3^2)
the distance; the distance traveled after three seconds is nine times
the distance traveled after one second. Finally, if an object travels
for four times the time, then it will cover 16 times (4^2) the distance;
the distance traveled after four seconds is 16 times the distance
traveled after one second. For objects with a constant acceleration, the
distance of travel is directly proportional to the square of the time
of travel.
Calculating the Average Acceleration
The average acceleration (a) of any object over a given interval of time (t) can be calculated using the equation
This equation can be used to calculate the acceleration of the object whose motion is depicted by the velocity-time data table
above. The velocity-time data in the table shows that the object has an
acceleration of 10 m/s/s. The calculation is shown below.
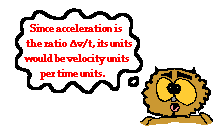 Acceleration values are expressed in units of velocity/time. Typical acceleration units include the following:
Acceleration values are expressed in units of velocity/time. Typical acceleration units include the following:
m/s/s
mi/hr/s
km/hr/s
m/s2
These units may seem a little awkward to a beginning physics student.
Yet they are very reasonable units when you begin to consider the
definition and equation for acceleration. The reason for the units
becomes obvious upon examination of the acceleration equation.
Since acceleration is a velocity change over a time, the units on
acceleration are velocity units divided by time units - thus (m/s)/s or
(mi/hr)/s. The (m/s)/s unit can be mathematically simplified to m/s2.
The Direction of the Acceleration Vector
Since acceleration is a vector quantity, it has a direction associated with it. The direction of the acceleration vector depends on two things:
-
whether the object is speeding up or slowing down
-
whether the object is moving in the + or - direction
 The general principle for determining the acceleation is:
The general principle for determining the acceleation is:
If an object is slowing down, then its acceleration is in the opposite direction of its motion.
This general principle can be applied to
determine whether the sign of the acceleration of an object is positive
or negative, right or left, up or down, etc. Consider the two data
tables below. In each case, the acceleration of the object is in the positive direction. In Example A, the object is moving in the positive direction (i.e., has a positive
velocity) and is speeding up. When an object is speeding up, the
acceleration is in the same direction as the velocity. Thus, this object
has a positive acceleration. In Example B, the object is moving in the negative direction (i.e., has a negative velocity) and is slowing down. According to our general principle, when an object is slowing down, the acceleration is in the opposite direction as the velocity. Thus, this object also has a positive acceleration.

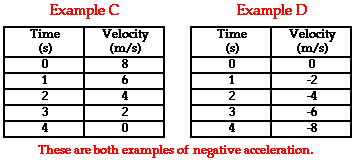
This same general principle can be applied to the motion of the objects
represented in the two data tables below. In each case, the acceleration
of the object is in the negative direction. In Example C, the object is moving in the positive direction (i.e., has a positive velocity) and is slowing down. According to our principle, when an object is slowing down, the acceleration is in the apposite direction as the velocity. Thus, this object has a negative acceleration. In Example D, the object is moving in the negative direction (i.e., has a negative
velocity) and is speeding up. When an object is speeding up, the
acceleration is in the same direction as the velocity. Thus, this object
also has a negative acceleration.

Observe the use of positive and negative as used in the discussion above
(Examples A - D). In physics, the use of positive and negative always
has a physical meaning. It is more than a mere mathematical symbol. As
used here to describe the velocity and the acceleration of a moving
object, positive and negative describe a direction. Both velocity and
acceleration are vector quantities and a full description of the
quantity demands the use of a directional adjective. North, south, east,
west, right, left, up and down are all directional adjectives. Physics
often borrows from mathematics and uses the + and - symbols as
directional adjectives. Consistent with the mathematical convention used
on number lines and graphs, positive often means to the right or up and
negative often means to the left or down. So to say that an object has a
negative acceleration as in Examples C and D is to simply say that its
acceleration is to the left or down (or in whatever direction has been
defined as negative). Negative accelerations do not refer acceleration
values that are less than 0. An acceleration of -2 m/s/s is an
acceleration with a magnitude of 2 m/s/s that is directed in the
negative direction.
Check Your Understanding
To test your understanding of the concept of acceleration, consider the
following problems and the corresponding solutions. Use the equation for
acceleration to determine the acceleration for the following two
motions.
 The
first six units of The Physics Classroom tutorial will involve an
investigation into the physics of motion. As we focus on the language,
principles, and laws that describe and explain the motion of objects,
your efforts should center on internalizing the meaning of the
information. Avoid memorizing the information; and avoid abstracting the
information from the physical world that it describes and explains.
Rather, contemplate the information, thinking about its meaning and its
applications.
The
first six units of The Physics Classroom tutorial will involve an
investigation into the physics of motion. As we focus on the language,
principles, and laws that describe and explain the motion of objects,
your efforts should center on internalizing the meaning of the
information. Avoid memorizing the information; and avoid abstracting the
information from the physical world that it describes and explains.
Rather, contemplate the information, thinking about its meaning and its
applications.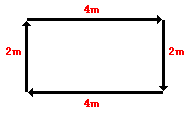
 Determining the Direction of the Velocity Vector
Determining the Direction of the Velocity Vector Since
a moving object often changes its speed during its motion, it is common
to distinguish between the average speed and the instantaneous speed.
The distinction is as follows.
Since
a moving object often changes its speed during its motion, it is common
to distinguish between the average speed and the instantaneous speed.
The distinction is as follows.
 Sports
announcers will occasionally say that a person is accelerating if
he/she is moving fast. Yet acceleration has nothing to do with going
fast. A person can be moving very fast and still not be accelerating.
Acceleration has to do with changing how fast an object is moving. If an
object is not changing its velocity, then the object is not
accelerating. The data at the right are representative of a
northward-moving accelerating object. The velocity is changing over the
course of time. In fact, the velocity is changing by a constant amount -
10 m/s - in each second of time. Anytime an object's velocity is
changing, the object is said to be accelerating; it has an acceleration.
Sports
announcers will occasionally say that a person is accelerating if
he/she is moving fast. Yet acceleration has nothing to do with going
fast. A person can be moving very fast and still not be accelerating.
Acceleration has to do with changing how fast an object is moving. If an
object is not changing its velocity, then the object is not
accelerating. The data at the right are representative of a
northward-moving accelerating object. The velocity is changing over the
course of time. In fact, the velocity is changing by a constant amount -
10 m/s - in each second of time. Anytime an object's velocity is
changing, the object is said to be accelerating; it has an acceleration.
 Acceleration values are expressed in units of velocity/time. Typical acceleration units include the following:
Acceleration values are expressed in units of velocity/time. Typical acceleration units include the following: The general principle for determining the acceleation is:
The general principle for determining the acceleation is:


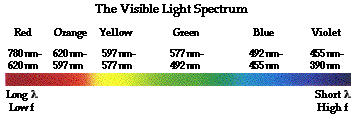
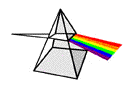 that specific color sensation. Isaac Newton showed that
that specific color sensation. Isaac Newton showed that 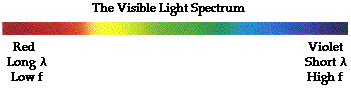
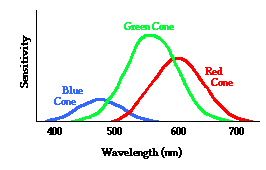
 physiological
occurs: photochemical reactions occur within the cones to produce
electrical impulses that are sent along nerves to the brain. The cones
respond to the incident light by sending a message forward to brain,
saying, "Light is hitting me." Upon reaching the brain, the
psychological occurs: the brain detects the electrical messages being
sent by the cones and interprets the meaning of the messages. The brain
responds by saying "it is white." For the case of white light entering
the eye and striking the retina, each of the three kinds of cones would
be activated into sending the electrical messages along to the brain.
And the brain recognizes that the messages are being sent by all three
cones and somehow interprets this to mean that white light has entered
the eye.
physiological
occurs: photochemical reactions occur within the cones to produce
electrical impulses that are sent along nerves to the brain. The cones
respond to the incident light by sending a message forward to brain,
saying, "Light is hitting me." Upon reaching the brain, the
psychological occurs: the brain detects the electrical messages being
sent by the cones and interprets the meaning of the messages. The brain
responds by saying "it is white." For the case of white light entering
the eye and striking the retina, each of the three kinds of cones would
be activated into sending the electrical messages along to the brain.
And the brain recognizes that the messages are being sent by all three
cones and somehow interprets this to mean that white light has entered
the eye.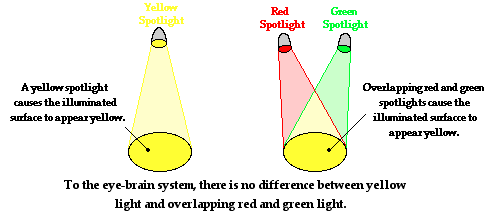
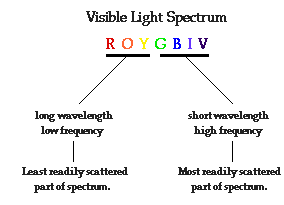
 wavelength.
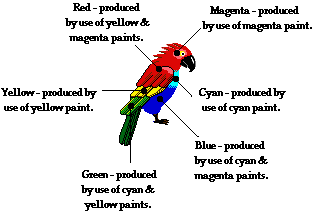
So technically, there is really no such thing as yellow light. Rather,
there is light with a wavelength of about 590 nm that appears yellow.
And there is also light with a mixture of wavelengths of about 700 nm
and 530 nm that together appears yellow. The yellow appearance of these
two clearly different light sources can be traced to the physiological
and psychological response of the eye-brain system, and not to the light
itself. So to be technically appropriate, a person would refer to
"yellow light" as "light that creates a yellow appearance." Yet, to
maintain a larger collection of friendships, a person would refer to
"yellow light" as "yellow light."
wavelength.
So technically, there is really no such thing as yellow light. Rather,
there is light with a wavelength of about 590 nm that appears yellow.
And there is also light with a mixture of wavelengths of about 700 nm
and 530 nm that together appears yellow. The yellow appearance of these
two clearly different light sources can be traced to the physiological
and psychological response of the eye-brain system, and not to the light
itself. So to be technically appropriate, a person would refer to
"yellow light" as "light that creates a yellow appearance." Yet, to
maintain a larger collection of friendships, a person would refer to
"yellow light" as "yellow light." ultimately
reflect or transmit it to our eyes. The color of an object is not
actually within the object itself. Rather, the color is in the light
that shines upon it and is ultimately reflected or transmitted to our
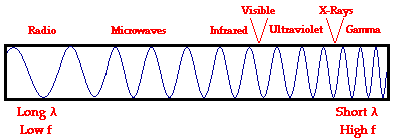
eyes. We know that the visible light spectrum consists of a range of
frequencies, each of which corresponds to a specific color. When visible
light strikes an object and a specific frequency becomes absorbed, that
frequency of light will never make it to our eyes. Any visible light
that strikes the object and becomes reflected or transmitted to our eyes
will contribute to the color appearance of that object. So the color is
not in the object itself, but in the light that strikes the object and
ultimately reaches our eye. The only role that the object plays is that
it might contain atoms capable of selectively absorbing one or more
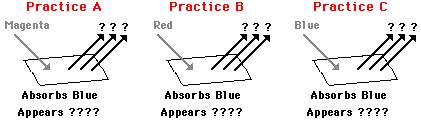
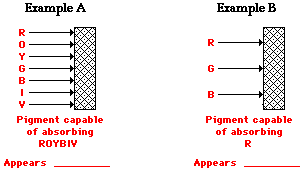
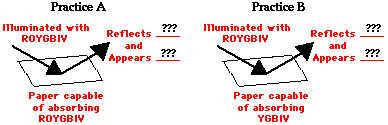
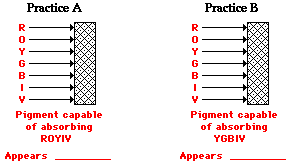
frequencies of the visible light that shine upon it. So if an object
absorbs all of the frequencies of visible light except for the frequency
associated with green light, then the object will appear green in the
presence of
ultimately
reflect or transmit it to our eyes. The color of an object is not
actually within the object itself. Rather, the color is in the light
that shines upon it and is ultimately reflected or transmitted to our
eyes. We know that the visible light spectrum consists of a range of
frequencies, each of which corresponds to a specific color. When visible
light strikes an object and a specific frequency becomes absorbed, that
frequency of light will never make it to our eyes. Any visible light
that strikes the object and becomes reflected or transmitted to our eyes
will contribute to the color appearance of that object. So the color is
not in the object itself, but in the light that strikes the object and
ultimately reaches our eye. The only role that the object plays is that
it might contain atoms capable of selectively absorbing one or more
frequencies of the visible light that shine upon it. So if an object
absorbs all of the frequencies of visible light except for the frequency
associated with green light, then the object will appear green in the
presence of 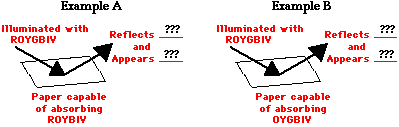
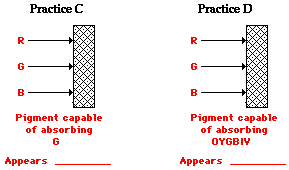
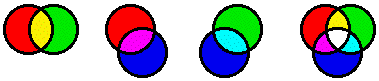
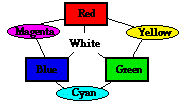
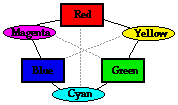
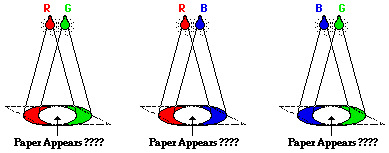
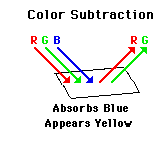
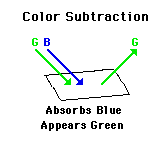
 students of physics, especially those who still believe that the color of a shirt is in the shirt itself. This is
students of physics, especially those who still believe that the color of a shirt is in the shirt itself. This is